
ستارگان
با دیدن این عکس از یک زمینه پرستاره، وسوسه می شویم که وسیلۀ اندازه تصویر یک ستاره دربارۀ اندازه آن ستاره قضاوت کنیم .اندازه تصویر، بیشتر با درخشندگی ظاهری ستاره رابطه مستقیمی دارد. اگر فاصله یک ستاره معلوم باشد، می توانیم درخشندگی آن را محاسبه کنیم. اما با توجه به رنگ ستاره می توانیم به طور تقریب درباره دمای سطح آن اظهارنظر کنیم؛ مثلاً رنگ مایل به سرخ ستاره نمایندۀ سردتر بودن و رنگ مایل به آبی نشانۀ داغتر بودن آن است.برای تعیین عواملی از قبیل جهت، فاصله،سرعت، اندازه، دما و درخشندگی ستارگان، اخترشناسان باید به طور کلی برتوانایی خود در تفسیر و تعبیر تابش هایی که از ستارگان دریافت می کنند، تکیه کنند.بسیاری از این عوامل به آگاهی ما از فاصله بستگی دارد. پس بهتر است نخست به روش تعیین فاصلۀ ستارگان نزدیک بپردازیم. نقشه پردازان برای اندازه گیری فاصله ای که بر روی زمین دوراز دسترس است، از روش مثلث بندی استفاده می کنند. مثلاً، فرض کنید می خواهیم فاصلۀ نقطۀ A از ساحل رود خانه ای را تا نقطه C واقع بر جزیره ای در میان رودخانه بدست آوریم (شکل زیر).
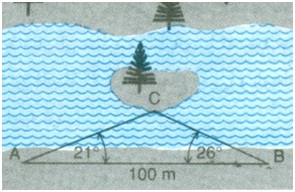
شکل ( زیر ) و به وسیله رادیو باهم ارتباط دارند. برای این کار در امتداد ساحل خط قاعدهAB را، مثلاًبه طول m100 مشخص می کنیم. سپس زاویه A و B را اندازه گیری و با استفاده از روابط مثلثاتی طول ضلع AC ، یعنی فاصله مورد نظر را محاسبه می کنیم. برای یافتن فاصله جسمی بسیار دور، آن جسم را ازدو محل متفاوت ( دو سر خطی که حکم قاعده را دارد. ) نگاه می کنیم، و هنگامی که ازیک سر خط به سر دیگر آن می رویم، زاویه ای را که به نظرمان می رسد جسم جابجا شدها ست، اندازه می گیریم . این زاویه را اختلاف منظر ستاره می نامیم.
برای تعیین فاصلۀ زمین تاماه فرض کنید دو ناظر در مواضع A و B روی زمین مستقر شده

ناظر A با رادیو اعلام می کند که ماه را باستاره D در یک خط می بیند وناظر B اعلام می کند که ماه را با ستاره C در یک خط می بیند، و بنابراین می تواند زاویه میان C و D را اندازهبگیرد. چون پرتوهای نور ستارۀ D برای هر دو ناظر موازی اند،متوجه می شویم که زاویه بین دو ستاره با زاویه ای برابر است که در ماه تشکیل می شود. بنا بر یک قضیه هندسی داریم که: زاویه های متبادل درونی خطوط موازی با هم برابرند. چون خط قاعدۀ AE ، یعنی شعاع زمین، مسافت معلومی است، محاسبۀ فاصلۀ A یا B تا ماه میسرمی شود. این روش، که اختلاف منظر زمین مرکزی نامیده می شود، به سبب کوتاه بودن نسبی خط قاعده آن فایده چندانی ندارد . اما، فایده این ایده را با بکار گرفتن خط قاعده بسیار درازتر- مثلاً به شعاع مدار زمین- می توان گسترش داد. ( شکل زیر).
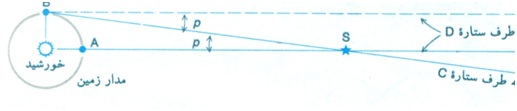
فرض کنید وقتی که زمین درموضع A است، ستاره نزدیک تر S با ستاره دورتر D هم خط باشد؛ اما سه ماه بعد، وقتی که زمین در B قرار دارد، ستاره S با ستاره C در یک خط باشند. در این صورت اخترشناس با اندازه گیری زاویۀ میان ستاره های C و D زاویه تشکیل شده درستاره S را می داند. این زاویه (P ) که اختلاف منظر خورشید مرکزی این ستاره نامیده می شود، همیشه کمتر از یک ثانیه ( درجه 3600/1 ) است. مثلث هایی با چنین زاویه کوچکی، را می توان با روش زیر حل کرد. دایره بسیار بزرگی را به مرکزستاره S و به شعاع فاصله r( شکل زیر ) را در نظر بگیرید.
خط قاعده (BF) جزء کوچکی از این دایره بزرگ و نسبت آن به کل محیط دایره برابر با نسبت زاویه اختلافنظر (P ) به کل 360 درجه دایره است؛که در این صورت خواهیم داشت:
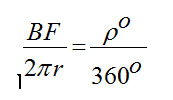
از این رابطه می توانیم r را به دست آوریم:
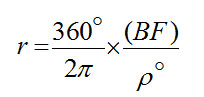
باتغییر واحد زاویه، به طوری که p بر حسب ثانیه باشد، و با انتقال ضریب 2 خواهیم داشت:
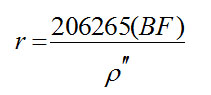
چون BF برابر AU 1 است، می توانیم r را بر حسب واحد نجومی به دست آوریم:
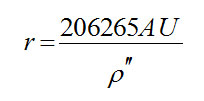
اگر AU 206265 را برابر یک پارسک بگیریم، رابطه بسیار ساده تری به دست می آوریم:
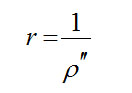
یک پارسک(parsec) عبارت است از فاصله ای که اگر ستاره ای در آن فاصله باشد، با استفاده از فاصله AU 1 به عنوان خط قاعده، اختلاف منظر خورشید مرکزی آن 1 ثانیه قوس می شود. واژۀ Parsec مخفف دوکلمهParallax ( اختلاف منظر) و Second (ثانیه) است. محاسبات بیشتر نشان می دهد که یک پارسک برابر است با 26ر3 سال نوری. توجه داشته باشید که هر چه فاصله (r ) تا ستاره بیشتر باشد، زاویه اختلاف منظر آن (p ) کوچکترخواهد شد. اختلاف منظر نزدیکترین ستاره به ما، پروکسیمای قنطورس، 75ر0 ثانیه قوس یاست، از این رو فاصله آن عبارت است از: 75ر0/1 =33ر1 پارسک یا 3ر4 سال نوری. برای ستارگانی به فاصله pc 100 (100 پارسک) زاویه اختلاف فقط برابر 01ر0 ثانیه(360000/1 درجه) است. اندازه گیری چنین زاویه های کوچکی با خطایای زیاد همراه است،به طوری که کارایی این روش را برای فواصل تقریباً بیش از pc 30 منتفی می کند. اما در این فاصله، اختلاف منظر هایی حدود 10000 ستارۀ اندازه گیری شده است.